深度学习

T4mako大约 16 分钟

深度学习

1、预备知识

https://zh.d2l.ai/chapter_preliminaries/index.htmlopen in new window

基础概念

梯度下降、误差、k 折交叉验证、过拟合与欠拟合、损失函数、向前传播、反向传播、计算图、激活函数

权重衰退：

使用均方范数作为硬性限制，控制模型复杂度，减少过拟合
通过限制参数值 w 的选择范围来控制模型容量 $||w||^2 \le \theta$ ，通常不限制 bias，小的 theta 意味着更强的正则项

dropout 丢弃法

动机：一个好的模型需要对输入数据的扰动鲁棒，减少过拟合

使用有噪音的数据等价于 Tikhonov 正则
dropout：在层之间加入噪音，丢弃一部分前一层的输入、后一层的输出

通常将 dropout 作用在 隐藏全连接层的输出 上，将其中的一些值随机设为 0 来控制模型复杂度，丢弃概率为 超参数，其他数会相应变大，保证均值方差一样

注意：dropout 用在训练模型上减少复杂性，在使用模型时一般不用 dropout

数值稳定性

数值稳定性常见的两个问题：

梯度爆炸
- 值超出阈值
- 对学习率敏感
梯度消失
- 梯度值变为 0
- 训练无进展
- 对于底部层尤为严重

因此，合理的权重初始值和激活函数的选取可以提升数值稳定性

数据集操作

数据集可分为

训练集
验证集
测试集

数据增广

数据增强：则国家已有数据集，使得有更多的多样性。如在语音中加入背景噪声、改变图片的颜色和形状（翻转、切割、改颜色）

数据增广一般使用 torchvision

硬件、计算性能

https://zh.d2l.ai/chapter_computational-performance/index.htmlopen in new window

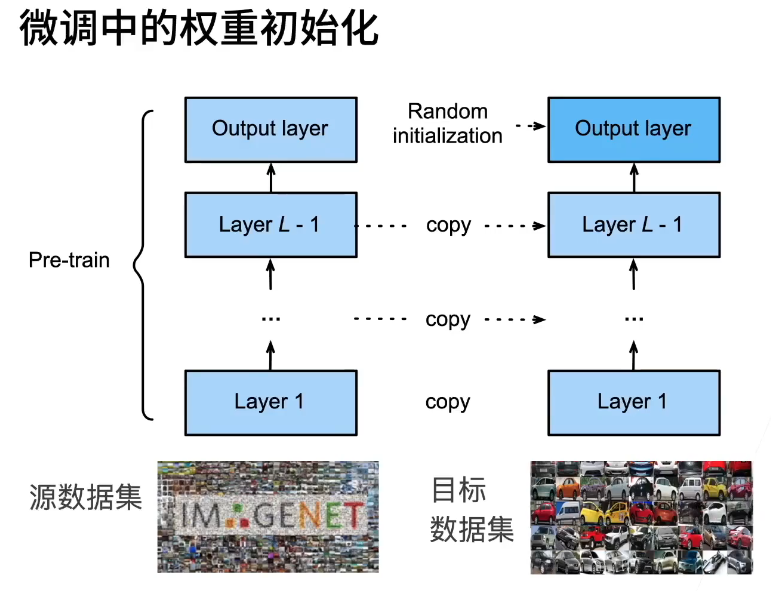
微调

使用已训练好的模型的特征提取层与权重，调整自己崔侯的全连接层

困惑度 perplexity

衡量一个语言模型的好坏可以用平均交叉熵
p 是语言模型的预测概率，x是真实词
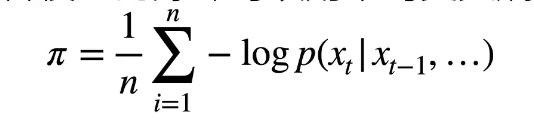
历史原因NLP使用困惑度 exp(a)来衡量，是平均每次可能选项。1表示完美，无穷大是最差情况

梯度剪裁

迭代中计算这 T 个时间步上的梯度，在反向传播过程中产生长度为O(T)的矩阵乘法链，导致数值不稳定
梯度裁剪能有效预防梯度爆炸、
如果梯度长度超过 0，那么拖影回长度0

2、线性神经网络

FNN（Feedforward Neural Network，前馈神经网络）：FNN 是一种神经网络架构，它按照层级顺序，将数据从输入层传递到输出层，每一层的节点连接到下一层的节点
MLP 是一种特定的 FNN，特点是包含至少一个隐藏层，且每一层的神经元是完全连接的

线性回归

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)  # y = 4 + 3 * X + 噪声

# 将数据转换为 PyTorch 张量
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.float32)

# 定义线性回归模型
class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1) #（输入维度，输出维度）输入x，输出y

    def forward(self, x):
        return self.linear(x)

# 实例化模型
model = LinearRegressionModel()

# 定义损失函数和优化器
criterion = nn.MSELoss()  # 均方误差损失
optimizer = optim.SGD(model.parameters(), lr=0.01)  # 随机梯度下降优化器

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    model.train()
    
    # 前向传播
    y_pred = model(X_tensor)
    
    # 计算损失
    loss = criterion(y_pred, y_tensor)
    
    # 反向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

# 绘制结果
model.eval()
with torch.no_grad():
    predicted = model(X_tensor).numpy()
plt.scatter(X, y, color='blue', label='实际数据')
plt.plot(X, predicted, color='red', label='拟合直线')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('线性回归示例')
plt.show()

Softmax 分类

Softmax 是多分类任务，隐藏层为线性层，输出为多个。

为了使输出为概率，使用 softmax $sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}} \quad \text{for } i = 1, 2, \ldots, K$ 函数，通过真实值与预测值的概率经过 交叉熵损失 得到 0,1 值

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader

# 1. 数据准备：下载MNIST数据集，并进行预处理
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))])

train_dataset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform)

train_loader = DataLoader(dataset=train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=64, shuffle=False)

# 2. 定义模型：一个简单的两层神经网络
class SimpleNet(nn.Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(28*28, 128)  # 输入层 (28*28像素)
        self.fc2 = nn.Linear(128, 10)     # 输出层 (10类)

    def forward(self, x):
        x = x.view(-1, 28*28)            # 将输入展平
        x = torch.relu(self.fc1(x))      # 第一个全连接层和ReLU激活函数
        x = self.fc2(x)                  # 第二个全连接层
        return torch.softmax(x, dim=1)   # 使用softmax函数生成概率分布

# 3. 初始化模型、损失函数和优化器
model = SimpleNet()
criterion = nn.CrossEntropyLoss()        # 交叉熵损失函数 (softmax和损失结合)
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 4. 训练模型
num_epochs = 5
for epoch in range(num_epochs):
    model.train()
    for images, labels in train_loader:
        outputs = model(images)          # 前向传播
        loss = criterion(outputs, labels) # 计算损失

        optimizer.zero_grad()            # 梯度清零
        loss.backward()                  # 反向传播
        optimizer.step()                 # 更新模型参数

    print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 5. 测试模型
model.eval()
correct = 0
total = 0
with torch.no_grad():
    for images, labels in test_loader:
        outputs = model(images)
        _, predicted = torch.max(outputs.data, 1)  # 预测最大概率的类
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print(f'Accuracy of the model on the 10000 test images: {100 * correct / total:.2f}%')

多层感知机 MLP

感知机为二分类。给定输入 x，权重 w，偏移 b，感知机输出 0 或 1（有时为 -1 或 1）。它不能拟合 XOR 函数

多层感知机（MLP）的简单例子：

import torch
import torch.nn as nn
import torch.optim as optim

# 定义MLP模型
class MLP(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(MLP, self).__init__()
        # 定义第一层全连接层
        self.fc1 = nn.Linear(input_size, hidden_size)
        # 激活函数ReLU
        self.relu = nn.ReLU()
        # 定义第二层全连接层
        self.fc2 = nn.Linear(hidden_size, output_size)
    
    def forward(self, x):
        # 第一层 + 激活函数
        out = self.fc1(x)
        out = self.relu(out)
        # 输出层
        out = self.fc2(out)
        return out

# 模型实例化
input_size = 10   # 输入特征数
hidden_size = 20  # 隐藏层神经元数
output_size = 3   # 输出类别数

model = MLP(input_size, hidden_size, output_size)

# 损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 假设我们有一个大小为10的输入张量
x = torch.randn(5, input_size)  # 批次大小为5
labels = torch.randint(0, output_size, (5,))  # 随机生成5个类别标签

# 前向传播
outputs = model(x)

# 计算损失
loss = criterion(outputs, labels)

# 反向传播和优化
optimizer.zero_grad()  # 梯度清零
loss.backward()        # 反向传播
optimizer.step()       # 更新参数

print(f'Loss: {loss.item()}')

3、卷积神经网络 CNN

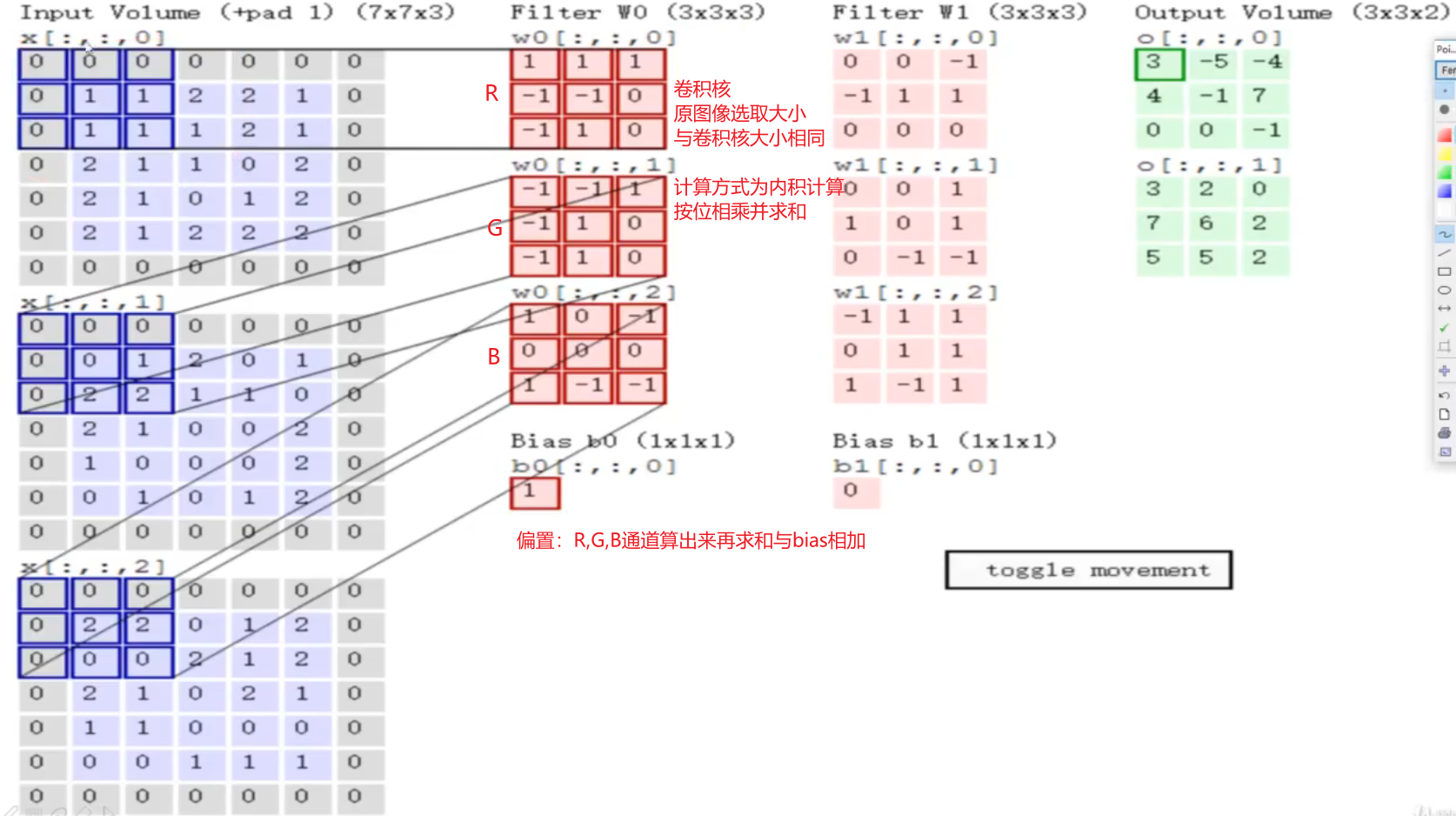
多输入输出通道

彩色图片由 RGB 三个通道，每个输入通道通常有独立的二维卷积核

可以使用多个三维卷积核（下图核函数粘贴复制），每个核生成一个输出通道

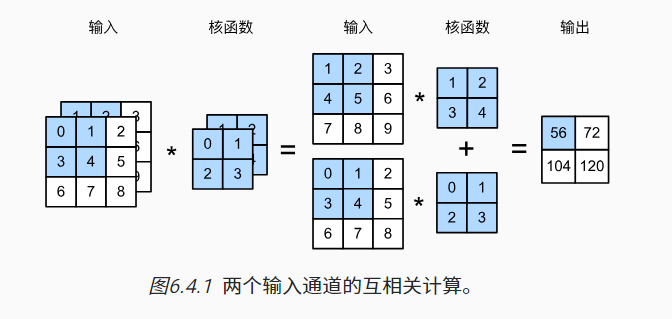
计算的结果为 特征图
一次卷积可以有多个 Filter，卷积后的深度就为 Filter 的个数（上述 7*7*3 经过 2 个 3*3*3 的 filter 变为 3*3*2 的特征图）

1 * 1 的卷积核不识别空间模式，只是融合通道，以 c_i 个输入 值转换为 c_o 个输出值

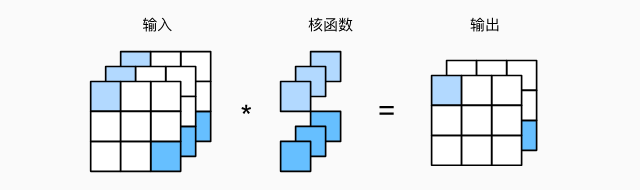
卷积层 conv（convolution）

卷积层中的 w 是卷积核，b 是偏置，w、b 是可学习参数

卷积层将输入和核矩阵进行交叉相关，加上偏移后得到输出
核矩阵和偏移是可学习的参数

卷积层 涉及 超参数：

滑动窗口步长
卷积核尺寸
是否边缘填充
卷积核个数

卷积层的权重（w + b）参数：所有卷积核的像素数 + 卷积核个数（偏置）

感受野（Receptive Field）：神经元「看到的」输入区域，在卷积神经网络中，feature map 上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野

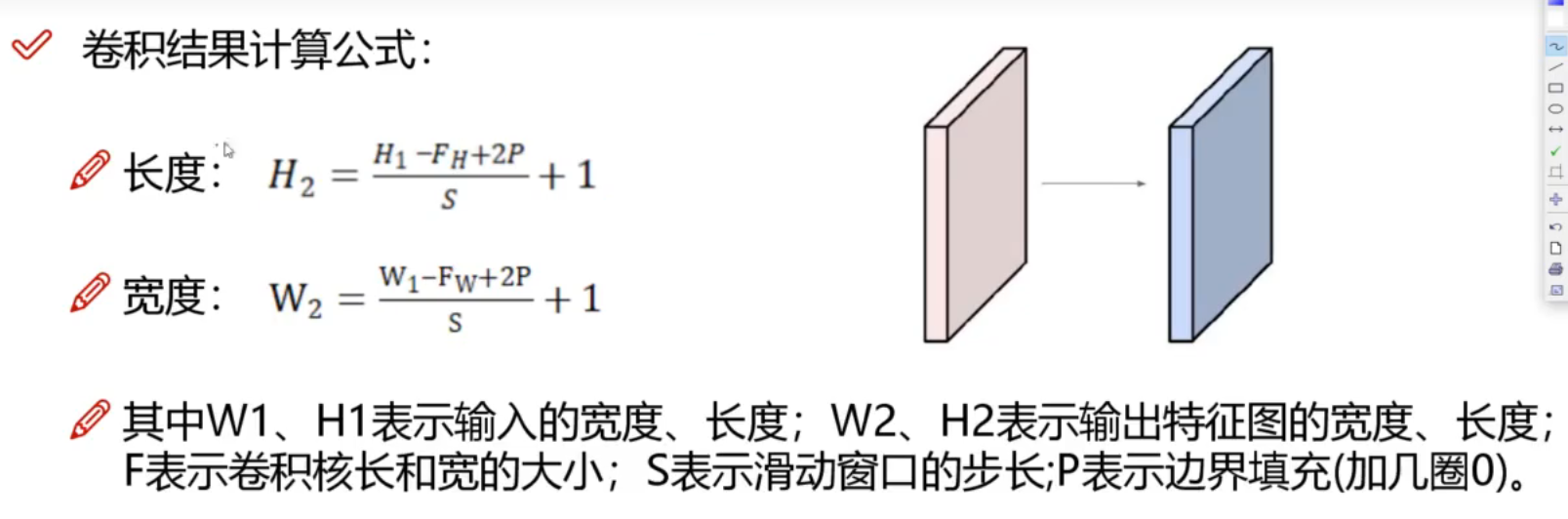
卷积结果计算公式：

可以对一次卷积后的特征图再卷积再卷积

池化层 pool

用于 压缩特征图

例如： MAX POOLING 最大池化层： 2*2 的特征为一组，筛选最大的值。平均池化层，将最大操作替换为平均

池化层与卷积层类似，都具有填充和步幅
池化层没有可学习的参数
在每个输入通道应用池化层以获得相应的输出通道
输出通道数 = 输入通道数

全连接层 fc

通过前面 conv 和 pool 得到最后的特征图（假设为 32*32*10），任务为 n 分类任务

将特征图拉成特征向量 [1,32*32*10] ，则全连接层参数为 [32*32*10,n]

4、经典卷积神经网络

LeNet （1980s）

卷积、全连接

AlexNet（2012 年）

更大卷积，全连接

Vgg（2014 年）

提出 vgg 块，更大更深的 AlexNet，赋值粘贴 AlexNet

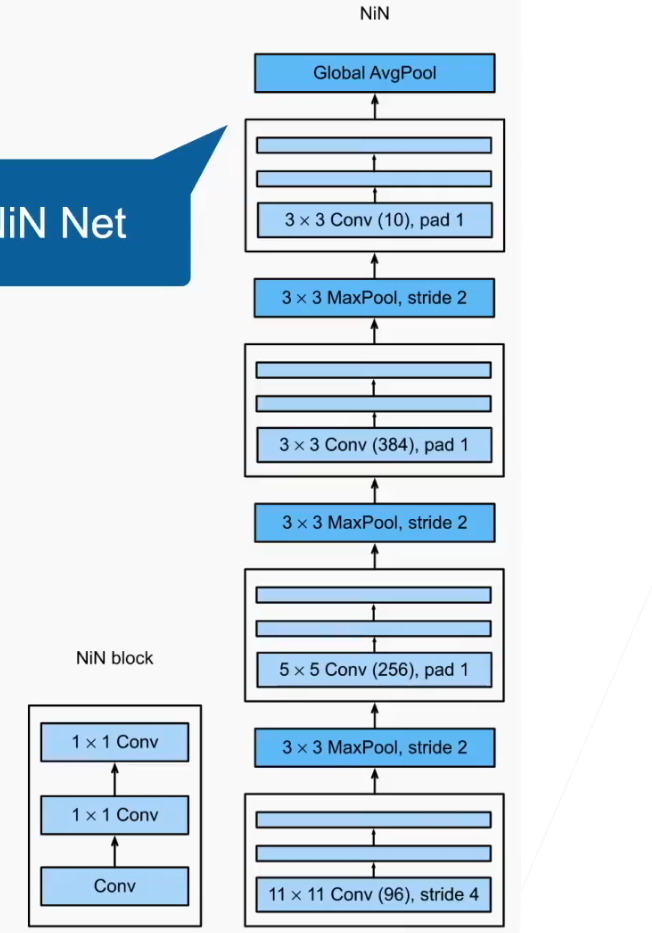
NiN

提出 NiN 块，一个卷积层后跟两个全连接层（1*1 的卷积核）

GoogLeNet

提出 Inception 块

Resnet（2015年）

vgg 在层数更多时，训练效果反而不好

resnet 将 好的层保留，不好的层跳过。做法是通过对层数堆叠的值与同等映射的值进行比较

若果层数堆叠的值不好，将层数堆叠权重设为 0

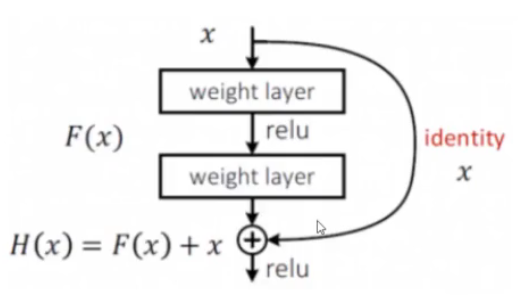
DenseNet

5、批量归一化层

损失在最后，后面的层训练比较快，前面的层训练比较慢。
前面的层一变化，所有层都得跟这边，最后的那些层需要重新学习多次，导致收敛边慢

归一化（Normalization）：将数据缩放到一个特定范围（通常是 [0, 1] 或 [-1, 1]） $x_{\text{normalized}} = \frac{x - x_{\min}}{x_{\max} - x_{\min}}$
标准化（Standardization）：将数据转化为均值为 0，标准差为 1 的标准正态分布。 $x_{\text{standardized}} = \frac{x - \mu}{\sigma}$
主要区别
特性 归一化 标准化
方法按最大值和最小值缩放按均值和标准差缩放
输出范围 [0, 1] 或 [-1, 1] 平均值 0，标准差 1
适用场景 特征范围有界，非正态分布的情况特征服从正态分布或算法对正态分布敏感
对异常值的敏感性 对异常值敏感相对较稳健

特性	归一化	标准化
方法	按最大值和最小值缩放	按均值和标准差缩放
输出范围	[0, 1] 或 [-1, 1]	平均值 0，标准差 1
适用场景	特征范围有界，非正态分布的情况	特征服从正态分布或算法对正态分布敏感
对异常值的敏感性	对异常值敏感	相对较稳健

方法：

固定 小批量 batch 里的均值和方差，然后再做额外调整
- 批量归一化层可学习的参数为 γ 和 β
- 作用在
  - 全连接层和卷积层输出上，激活函数前
  - 全连接层和卷积层输入上
- 对全连接层，作用在特征维
- 对于卷积层，作用在通道维

6、循环神经网络 RNN

https://www.bilibili.com/video/BV1z5411f7Bm/open in new window

在时间序列上，隐藏层与隐藏层之间包含关系 W_i

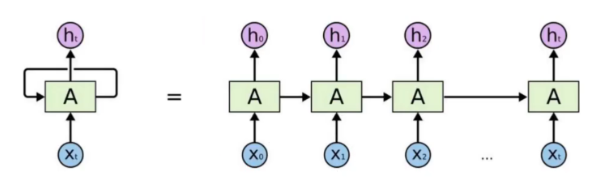
RNN 在计算梯度时容易发生梯度爆炸‘

解决梯度爆炸的方法：

梯度裁剪：梯度裁剪通过设定一个阈值来限制梯度的大小。如果梯度超过这个阈值，它们将被缩放至阈值以内，从而避免了大的权重更新。这样做有助于稳定训练过程

7、经典循环神经网络

RGN

LSTM

相较于 RNN，添加控制参数 c，决定什么样的信息会被保留，什么样的会被遗忘

https://www.bilibili.com/video/BV1Z34y1k7mcopen in new window

深度循环神经网络

双向循环神经网络

编码器-解码器架构

编码器、解码器架构：一个模型被分为两块：

编码器 Encoder 处理输出（类似 CNN 提取特征）
解码器 Decoder 生成输出（类型 fc 进行预测）

机器翻译是序列转换模型的一个核心问题，其输入和输出都是长度可变的序列。为了处理这种类型的输入和输出，我们可以设计一个包含两个主要组件的架构：

第一个组件是一个编码器（encoder）：它接受一个长度可变的序列作为输入，并将其转换为具有固定形状的编码状态。
第二个组件是解码器（decoder）：它将固定形状的编码状态映射到长度可变的序列。这被称为编码器-解码器（encoder-decoder）架构

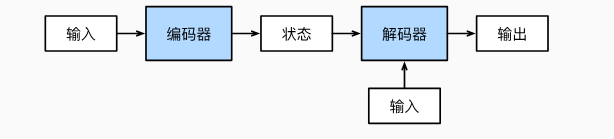
“编码器－解码器”架构可以将长度可变的序列作为输入和输出，因此适用于机器翻译等序列转换问题。
编码器将长度可变的序列作为输入，并将其转换为具有固定形状的编码状态。
解码器将具有固定形状的编码状态映射为长度可变的序列。

seq2seq

根据“编码器-解码器”架构的设计，我们可以使用两个循环神经网络来设计一个序列到序列学习的模型。
在实现编码器和解码器时，我们可以使用多层循环神经网络。
我们可以使用遮蔽来过滤不相关的计算，例如在计算损失时。
在“编码器－解码器”训练中，强制教学方法将原始输出序列（而非预测结果）输入解码器。
BLEU是一种常用的评估方法，它通过测量预测序列和标签序列之间的 n 元语法的匹配度来评估预测。

8、注意力机制

注意力机制

卷积、全连接、池化都只考虑「不随意线索」
注意力机制则显示的考虑随意线索
- 注意力 attention 即权重

非参注意力池化层

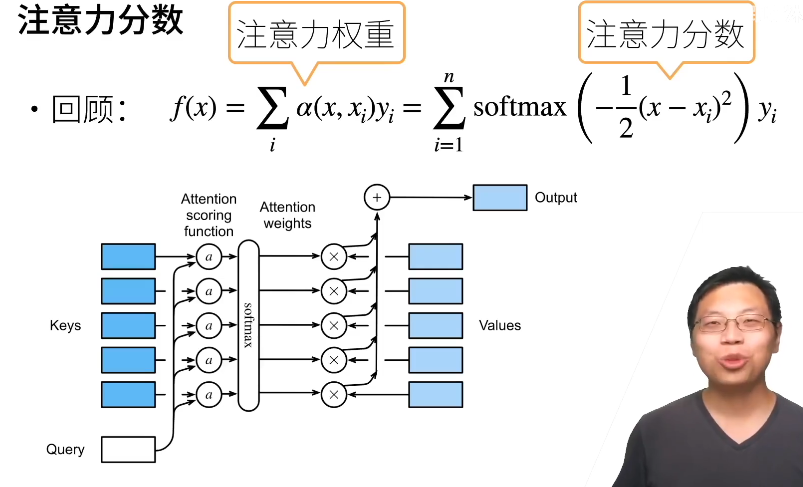
注意力分数

注意力分时是 query 和 key 的相似度，注意力权重是分时的 sofrmax 结果
两种常见的分数计算：
- 将 query 和 key 合并起来进入一个单输出单隐藏层的 MLP
- 直接将 query 和 key 做内积

自注意力机制 slef-attention

给定序列 $x_1,x_2,...x_n$ ， $x_i$ 为向量
自注意力机制池化层将 $x_i$ 当做 key，value，query 来对序列抽取特征得到 $y_1,...y_n$ ，这里 $y_i = f(x_i,(x_1,x_1),...,(x_n,x_n))$
self 即 key，value，query 都是自己取的
完全并行、最长序列为 1、但对长序列计算复杂度高
位置编码在输入中加入位置信息，使得自注意能够记忆位置信息

9、Transformer

LSTM 的训练是迭代的、串行的，必须要等当前字处理完，才可以处理下一个字

Transformer 的训练时并行的，即所有字是同时训练的，这样大大增加了计算效率
Transformer 使用了位置嵌入(Positional Encoding)来理解语言的顺序，使用自注意力机制（Self Attention Mechanism）和全连接层进行计算

Transformer **Encoder **负责把输入（语言序列）隐射成 隐藏层（下图中第2步用九宫格代表的部分），然后解码器 Decoder 再把隐藏层映射为自然语言序列。例如下图机器翻译的例子

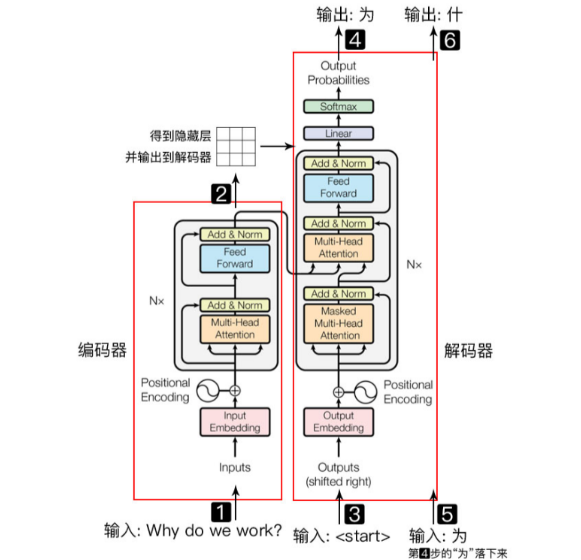
Encoder Block 结构图：

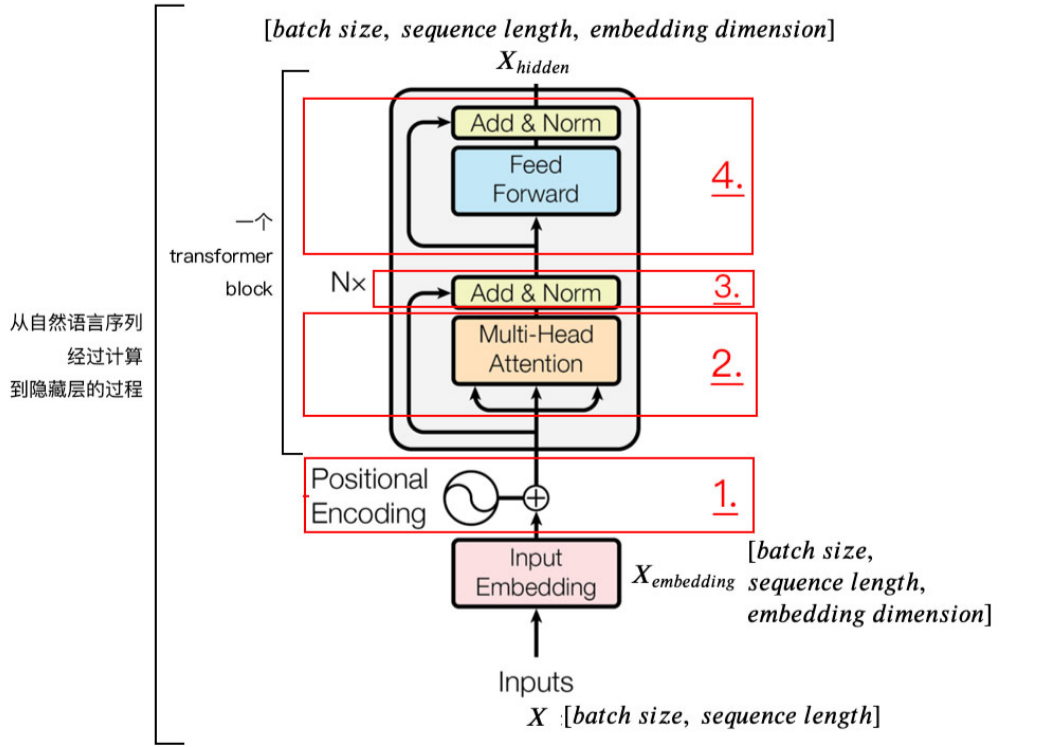
1. Positional Encoding

Transformer 没有 RNN 的迭代操作（在时间上递归）
所以我们必须提供每个字的 位置信息 给 Transformer，这样它才能识别出语言中的顺序关系

2、自注意力机制 Self Attention Mechanism

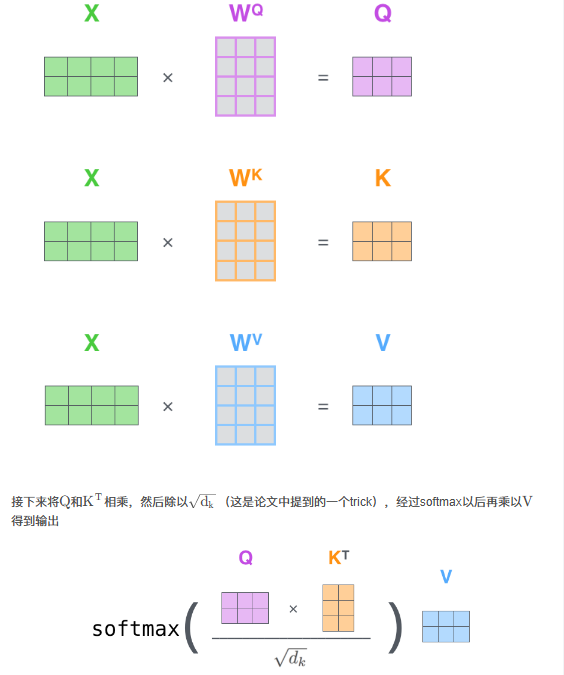
对于输入的句子 X：

通过 WordEmbedding 得到字的 字向量
通过 Positional Encoding 得到字的 位置向量，
两者相加（维度相同，可以直接相加），得到该 字真正的向量表示。第 t 个字的向量记作 x_t

定义三个矩阵（变量 w） W_Q，W_k，W_v，使用这三个矩阵分别对所有的 字向量 进行三次线性变换，得到新的向量 q_t， k_t，v_t

将所有 q_t 拼接成一个大矩阵，记作 查询矩阵 Q
将所有 k_t 拼接成一个大矩阵，记作 键矩阵 K
将所有 v_t 拼接成一个大矩阵，记作 值矩阵 V

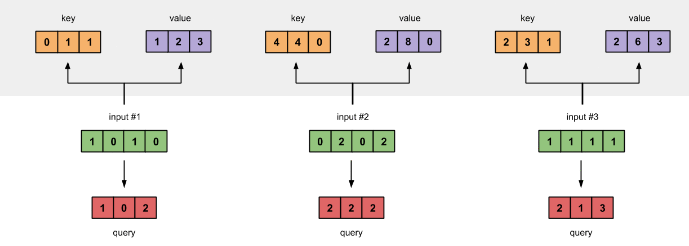
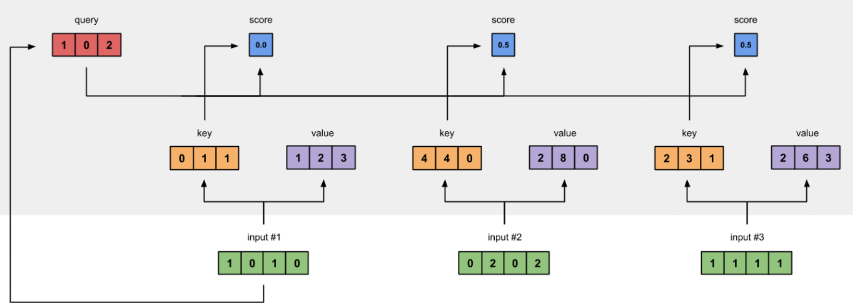
为获得第一个字的 注意力权重，需要用第一个字的查询向量 q₁ 乘以键矩阵 K

注意力权重：衡量输入序列中每个位置对其他位置的重要性。通过这些权重，模型可以动态地关注序列中不同部分的信息，从而更好地处理任务，如机器翻译、文本生成或图像处理

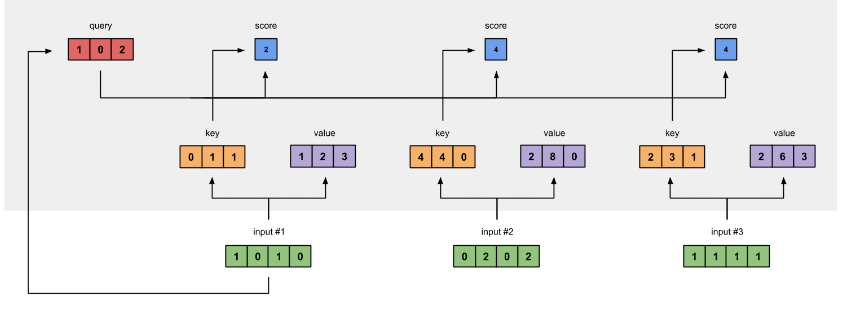
将得到的值经过 softmax，使得它们的和为1 softmax([2, 4, 4]) = [0.0, 0.5, 0.5]

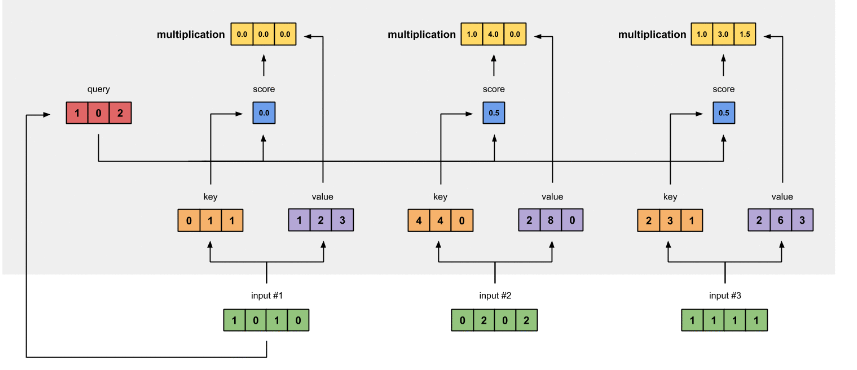
有了权重之后，将权重其分别乘以对应字的 值向量 v_t

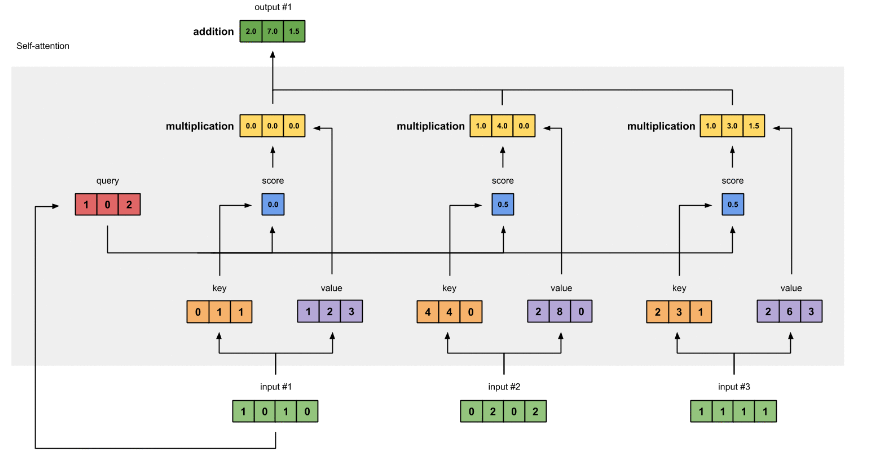
将这些 权重化后的值向量求和，得到第一个字的输出

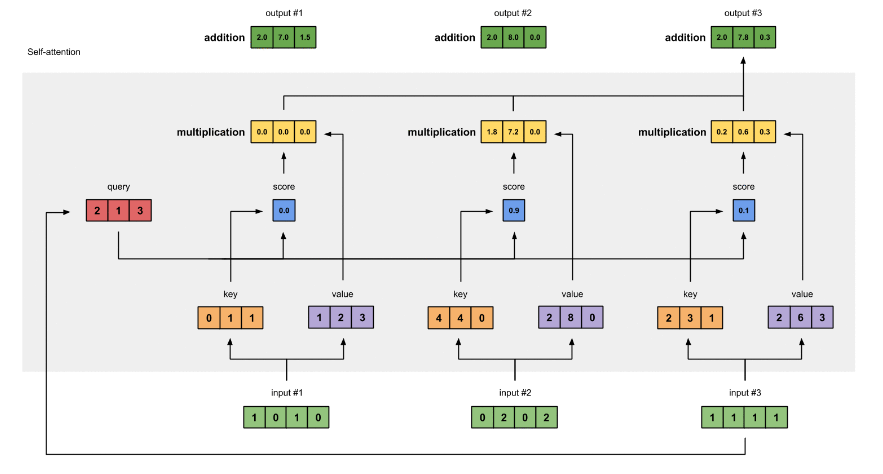
对其它的输入向量也执行相同的操作，即可得到通过 self-attention 后的所有输出

矩阵形式：

3、Multi-Head Attention 多头注意力

可以定义多组 Q，K，V，让它们分别关注不同的上下文。计算 Q，K，V 的过程还是一样。线性变换的矩阵从一组（W^Q,W^k,W^v）变成了多组（W^Q₀,W^k₀,W^v₀）,（W^Q₁,W^k₁,W^v₁）

对于输入矩阵 X，每一组Q、K 和 V 都可以得到一个输出矩阵 Z

4、残差连接和 Layer Normalization

残差连接

在上一步得到经过 self-attention 加权输出（Attention(Q,K,V)）后，把他们加起来做残差连接

X_{embedding} + Self Attention(Q,K,V)

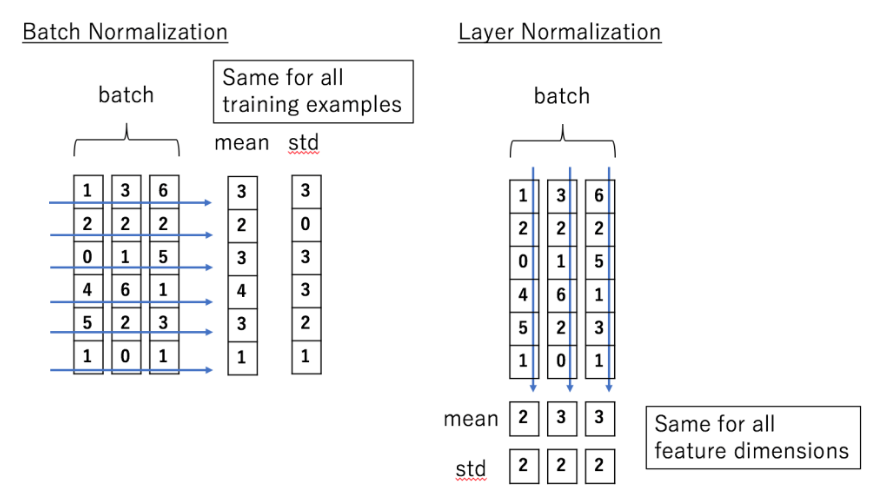
Layer Normalization

Layer Normalization 的作用是把神经网络中隐藏层归一为标准正态分布，以起到加快训练速度，加速收敛的作用

以矩阵的列(column)为单位求均值

\mu _j = \frac{1}{m}\sum_{i=1}^{m}X_{ij}

以矩阵的列(column)为单位求方差

\sigma _j^2 = \frac{1}{m}\sum_{i=1}^{m}(X_{ij}-\mu_j)^2

用每一列的每一个元素减去这列的均值，再除以这列的方差，从而得到归一化后的数值，加 $\xi $ 是为了防止分母为 0

LayerNorm(x) = \frac{X_{ij}-\mu{j}}{\sqrt{\sigma_j^2+\xi}}

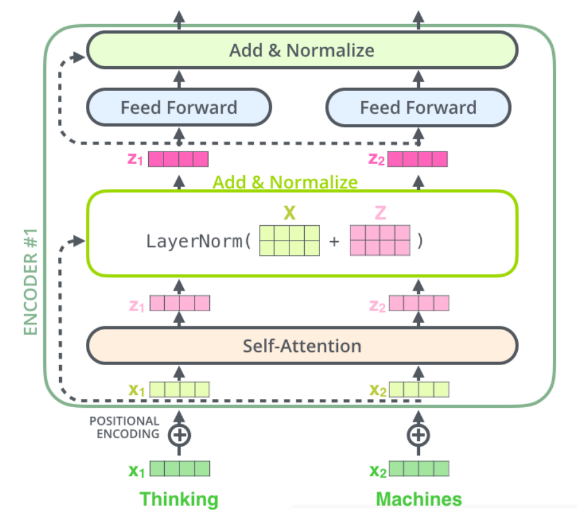
5、Transformer Encoder 整体结构

用公式把一个 Encoder block 的计算过程整理一下：

字向量与位置编码
$X = Embedding Lookup(X) + Position Encoding$
自注意力机制
$Q = Linear(X) = XW_Q \\ K = Linear(X) = XW_K \\ V = Linear(X) = XW_V \\ X_{attention} = SelfAttentnion(X_{attention})$
self-attention 残差连接与 Layer Normalization
$X_{attention} = X + X_{attention} \\ X_{attention} = LayerNorm(X_{attention})$
FeedForward，其实就是两层线性映射并用激活函数激活，比如说 ReLU
$X_{hidden} = Linear(ReLU(Linear(X_{attention})))$
FeedForward残差连接与Layer Normalization
$X_{hidden} = X_{attention} + X_{hidden} \\ X_{hidden} = LayerNorm(X_{hidden})$

昵称

邮箱

网址

按正序
按倒序
按热度

深度学习

# 深度学习

# 1、预备知识

# 基础概念

# 数据集操作

# 数据增广

# 硬件、计算性能

# 微调

# 困惑度 perplexity

# 梯度剪裁

# 2、线性神经网络

# 线性回归

# Softmax 分类

# 多层感知机 MLP

# 3、卷积神经网络 CNN

# 多输入输出通道

# 卷积层 conv（convolution）

# 池化层 pool

# 全连接层 fc

# 4、经典卷积神经网络

# LeNet （1980s）

# AlexNet（2012 年）

# Vgg（2014 年）

# NiN

# GoogLeNet

# Resnet（2015年）

# DenseNet

# 5、批量归一化层

# 6、循环神经网络 RNN

# 7、经典循环神经网络

# RGN

# LSTM

# 深度循环神经网络

# 双向循环神经网络

# 编码器-解码器架构

# seq2seq

# 8、注意力机制

# 注意力机制

# 注意力分数

# 自注意力机制 slef-attention

# 9、Transformer

# 1. Positional Encoding

# 2、自注意力机制 Self Attention Mechanism

# 3、Multi-Head Attention 多头注意力

# 4、残差连接和 Layer Normalization

# 残差连接

# Layer Normalization

# 5、Transformer Encoder 整体结构

预览:

深度学习

1、预备知识

基础概念

数据集操作

数据增广

硬件、计算性能

微调

困惑度 perplexity

梯度剪裁

2、线性神经网络

线性回归

Softmax 分类

多层感知机 MLP

3、卷积神经网络 CNN

多输入输出通道

卷积层 conv（convolution）

池化层 pool

全连接层 fc

4、经典卷积神经网络

LeNet （1980s）

AlexNet（2012 年）

Vgg（2014 年）

NiN

GoogLeNet

Resnet（2015年）

DenseNet

5、批量归一化层

6、循环神经网络 RNN

7、经典循环神经网络

RGN

LSTM

深度循环神经网络

双向循环神经网络

编码器-解码器架构

seq2seq

8、注意力机制

注意力机制

注意力分数

自注意力机制 slef-attention

9、Transformer

1. Positional Encoding

2、自注意力机制 Self Attention Mechanism

3、Multi-Head Attention 多头注意力

4、残差连接和 Layer Normalization

残差连接

Layer Normalization

5、Transformer Encoder 整体结构